5.5 電子

目次 ／ 第5章：微視的粒子

読者ガイド：なぜ「点状電子」の直観だけでは足りないのか

以下の「不足」は計算の失敗ではありません。起源や構造のイメージが弱い領域を指し示します。そこで本稿では、既存の数値と整合させたまま、近傍を環状として描く図像を補います。

• 電荷の由来が見えないこと。 点状の言葉は電荷を内在的定数として扱いますが、なぜ大きさや符号がそうなるのかは示しません。
• 量子数の「なぜ」。 スピン 1/2 と電荷量子化は規則として機能しますが、電子が「何に似ているか」の手触りは弱いままです。
• 近傍幾何の読みにくさ。 実験は遠方場や超短時間の高エネルギーを主に検証し、点状の外観になります。同一幾何で電場と磁場がどう結びつくかは、図像化されにくいのが現状です。
• 古典的直観の罠。 回転する帯電球体の絵は相対論・放射反作用・散乱限界に反します。正しく棄却されますが、初心者には誘惑的です。
• 放射反作用の語りにくさ。 量子的な扱いは整っていますが、純古典方程式は先行加速や暴走解を許し、媒質と記憶を用いた直観的再叙述を望ませます。

要するに、点状モデルは数値面で強力です。**エネルギー糸理論（EFT）**は、これらを否定せず、近傍の説明力を補うために環状の描像を加えます。

核心アイデア（読者向け）

本稿の枠組みでは、電子は幾何学的点ではなく、一本のエネルギー糸（Energy Threads）がエネルギー海（Energy Sea）の中で自立する単一閉環です。環には有限の厚みがあり、断面では位相がロックされた螺旋流が内側ほど強く外側ほど弱く巡ります。この近傍構造は媒質に内向きの指向テクスチャを刻みます。これを負電荷の操作的定義とします。一方で、環に沿うロック循環と全体指向の時間平均（ゆるやかな歳差と微小ゆらぎ。剛体の 360° 回転ではありません）により、遠方ではほぼ等方な穏やかな牽引へと平滑化され、質量として現れます。さらに閉じた循環とその拍節は、それぞれスピンと磁気モーメントとして観測されます。

読者への注意：ここでいう「位相バンドが走る」とはモード前線の伝播を指し、物質や情報の超光速伝送を意味しません。

I 電子はどう「結ばれる」か：環の閉成と断面螺旋

1. 基本像
   • 適切な**密度（Density）と張力（Tension）**の条件では、エネルギー海が糸を「引き上げ」ます。糸は最小労力の経路を選び、単一環として閉じて長寿化します。
   • 環は弾性的で有限厚をもち、幾何と張力の釣り合いが安定を与えます。
   • 断面では位相が螺旋状にロック循環し、内側に長く外側に短く滞在します。静止模様ではなく、高速で連続的な位相バンドです。
   • 環方向の拍節は速く、全体指向はゆっくり歳差し微小にゆらぎます。時間平均すると遠方は軸対称の外観となり、剛体回転を仮定する必要はありません。
2. 極性と離散性の手がかり
   • 負電荷は、視線に依存せず環の内側を向く近傍テクスチャによって定義します。
   • その鏡像として「外強内弱」の断面は外向きの矢印を刻み、正電荷に対応します。同一外場で応答の符号は鏡像になります。
   • 安定なのは限られたロック段（ステップ）と編み様式だけで、最小段が1 単位の負電荷に対応します。複雑な段はコストが高く長寿命になりにくいです。
3. 安定化の窓
   環として閉じ、自己張力が釣り合い、位相がロックし、適切な寸法とエネルギーをもち、環境のせん断が閾値を超えない――これらを同時に満たすときだけ「電子」になります。多くは短命に海へ崩れ、少数が窓に入り長生きします。

II 質量はどう見えるか：対称な「浅い鉢」

1. 張力地形
   エネルギー海の上に環を置くのは、張られた膜に対称な浅い鉢を軽く押し込むのに似ています。環近傍で最も張られ、外側へ急速に平坦化します。
2. これが質量と読める理由
   • 慣性：電子を動かすと、鉢と周囲の媒質も一緒に引きずられ、四方から引き戻しが生じます。環が締まるほど鉢は深く安定になり、慣性が大きくなります。
   • 案内（重力様）：同じ構造が周囲の張力地図を書き換え、電子へ向かう緩やかな斜面を作ります。通過する粒子や波束は、その斜面に案内されやすくなります。
   • 等方性と等価性：遠方外観は偏らず、等方性試験や等価原理と整合します。
   • 統計的張力重力：多数の微小構造を時空平均すると、穏やかで統一的な案内効果として表れます。

III 電荷はどう見えるか：近傍の「内向き渦」と中間距離の凝集

この図像では、電場は指向テクスチャの半径方向の延長、磁場は運動や内部循環による方位（アジマス）方向の巻き返しです。どちらも近傍幾何に同源で、役割が異なります。

• 近傍の内向き渦
  「内強外弱」の断面は、媒質に内向きのテクスチャを刻みます。このテクスチャと整合する構造体は流路抵抗が小さく、統計的に引力が現れます。不整合なら抵抗が大きくなり斥力に見えます。非構造的な波束に対してはこのチャネル効果は弱く、主に浅い鉢としての質量項が支配します。
• 運動と磁場
  電子が並進すると、テクスチャは速度方向に引きずられ、経路の周りで方位方向に巻き返します。これが磁場の外観です。並進がなくても、内部のロック循環は局所的巻き返しを組織し、固有磁気モーメントに対応します。幾何学的半径に依らないことを強調するため、等価循環／トーラス束と呼びます。高エネルギー・短時間窓では外観は近似点状へ復帰します。
• 雑音レベルの微調整
  海のバックグラウンド雑音は、この「内向き渦」をわずかに変調し得ます。観測されるなら、可逆・再現・オン／オフ可能で、制御された張力勾配（Tension Gradient）に線形であり、既存上限を十分下回ることが要件です。

IV スピンと磁気モーメント：単一環の拍節と位相ロック

• スピンの直観的定義
  スピンは、閉じたキラルな位相拍節の時間平均された外在化として読みます。剛体回転そのものではありません。
• 磁気モーメントの起源と向き
  モーメントは等価循環／トーラス束から生じ、可観測な幾何半径を前提としません。大きさと方向は、環方向の拍節、「内強外弱」の偏り、近傍テクスチャの秩序から決まります。
• 外場中の歳差と応答
  外部の指向ドメインが変わると歳差が生じ、遷移準位や線形が較正可能なシフトを示します。速度は内部ロックの強さと外部勾配で決まります。

V 三つの重ね図：環ドーナツ → 柔らかな縁の枕 → 対称な浅い鉢

• 近景（ミクロ）
  環ドーナツ。環上の帯がもっとも張られ、断面の螺旋は内強外弱が明瞭です。近傍には内向き矢印のテクスチャが現れ、負電荷の符号を固定します。
• 中景（遷移層）
  柔らかな縁の枕。時間を長く平均すると細かな紋理はなだらかになり、電荷分布はより凝集して見えます。
• 遠景（マクロ）
  対称な浅い鉢。縁の深さはほぼ一様で、質量外観は安定かつ等方的です。

図示の目印：「位相前線の短弧＋トレイル」「内向き矢印」「遷移枕の外縁」「鉢の口径と等深リング」。凡例：「等価循環（幾何半径に依存しない）」「時間平均後の等方性」。

VI スケールと可観測性：中核は極小、ただし「側写」は可能

• 極小コア
  巻き込まれた中核は非常に緻密で、現状のイメージングでは分解困難です。高エネルギー・超短時間では点状応答が優勢になります。
• 実効電荷半径のプロファイル
  近傍の内向き渦と中距離の凝集は、実効電荷が環域に寄ることを示唆します。高精度の弾性散乱や偏光測定によって、この**「実効半径」を側写**できます。
• 点状極限（強いコミット）
  現行のエネルギー域・時間窓では、形状因子は点状外観へ収束し、追加の解像可能な紋理は生じません。いわゆる実効半径はエネルギーとともに不可分解へ向かいます。
• 滑らかな遷移
  近から遠へは連続的に平滑化され、遠方では安定な鉢のみが見え、走る位相バンドは見えません。

VII 生成と対消滅：どう生まれ、どう消えるか

• 生成
  高張力・高密度の事象で、断面螺旋を巻き込んで固定する「巻き窓」が開きます。「内強外弱」に固定されれば負電荷が確定し、外強内弱なら陽電子が得られます。
• 対消滅
  電子と陽電子が接近すると、互いの近傍「渦」は相殺され、閉じたネットワークは短時間で解体されます。張力は波束として海へ戻り、光などの放出として観測されます。エネルギーと運動量は、糸と海の間で項ごとに保存されます。

VIII 現代理論との対応表

1. 一致する点
   • 電荷の量子化と同一性：最小段の「内強」ロックは、実験と合う1 単位の負電荷に対応します。
   • スピンと磁気モーメントの結伴：閉循環と拍節は、両者の自然な共起を与えます。
   • 散乱での点状外観：極小コアと時間平均により、高エネルギー散乱は近似点状となります。
2. 新しく可視化される層
   • 電荷起源の絵：負電荷は断面螺旋の半径方向の偏りが刻む内向き指向に直接由来し、事後のラベル付けではありません。
   • 質量と案内の統一図：対称な浅い鉢＋時間平均により、近傍の異方性と遠方の等方性を一枚に統合します。
   • 電磁の統一スケッチ：電気は半径方向の延長、磁気は方位方向の巻き返しであり、いずれも近傍幾何と観測時間窓から生じます。
3. 整合性と境界条件
   • 高エネルギー整合：現在の窓では形状因子は点状へ戻り、追加の模様は現れません。
   • 磁気モーメントのベンチマーク：大きさと方向は測定と一致し、環境依存の微小偏差は可逆・再現・較正可能で、現不確かさの下であるべきです。
   • 電気双極子モーメント（EDM）のほぼゼロ：一様環境ではほぼゼロ。制御された張力勾配（Tension Gradient）下ではごく弱い線形応答を許容しますが、現行上限未満に収まる必要があります。
   • 分光学の維持：水素様スペクトル、微細・超微細構造、干渉計の結果は誤差帯内にとどまります。新特徴は独立検証とオン／オフ判定を要します。
   • 動的安定性：因果に反する先行効果や自発的暴走はありません。散逸がある場合は、糸—海結合の因果記憶として表れ、その時間スケールは較正可能で観測と矛盾しません。

IX 観測可能な読み取り線：像面｜偏光｜時間｜スペクトル

• 像面：束の偏向や内縁の強調は、鉢の幾何と電荷の凝集を示唆します。
• 偏光：偏光散乱では、内向きテクスチャと整合するバンドや位相差が、近傍の幾何学的指紋として現れ得ます。
• 時間：局所閾値を越えるパルス励起で段差やエコーが現れる可能性があります。時定数はロック強度に従います。
• スペクトル：再処理環境では、「内強」由来のソフト領域の持ち上がりと狭いハードピークが共存し得ます。微小シフトや分裂は、ロック強度の雑音的微調整を反映します。

X 予測と検証：近傍・中間場に向けた操作的プローブ

• 近傍散乱におけるキラリティ反転
  予測：プローブのキラリティを反転、または電子を陽電子に置換すると、位相シフトが対で反転します。
  装置：単一粒子トラップと、軌道角運動量をもつマイクロ波／光学モード（キラリティ切替可能）。
  判定：可逆な反転で安定した振幅。
• 有効 g 因子の環境線形ドリフト
  予測：制御された張力勾配下でサイクロトロン周波数に微小な線形ドリフトが生じ、陽電子では符号が反転します。
  装置：高安定磁気トラップと、勾配を較正する微小質量体／マイクロキャビティ場。
  判定：ドリフトは勾配に一次比例し、正負粒子で鏡像。
• ほぼゼロの EDM と勾配誘起の線形応答
  予測：一様場ではほぼゼロ。勾配をかけるとごく弱い可逆応答が現れます。
  装置：イオントラップ／分子ビームに等価張力勾配を重畳し、共鳴位相法で読み出します。
  判定：勾配のオン／オフと向きで可逆、振幅は上限未満。
• キラル・ナノ細孔での非対称透過
  予測：事前偏極した電子がキラル境界を通過すると、出射角分布にごく小さな左右非対称が生じ、陽電子で反転します。
  装置：キラル・ナノ膜、多角度・多エネルギーの走査。
  判定：非対称成分は膜のキラリティと粒子の極性に同調。
• 強場放射の微小バイアス
  予測：強い曲率の場で放射角分布に、内向きテクスチャの手性と一致する再現性ある微小バイアスが現れます。
  装置：蓄積リングでの e⁻/e⁺ 比較（偏極・角度分布）、または超高強度レーザーでの反跳幾何の測定。
  判定：差異はエネルギーに対して較正可能で、正負で符号反転。

用語ミニガイド（読者向け）

• エネルギー糸（Energy Threads）：位相と張力を担う線状キャリア。有限の厚みをもちます。
• エネルギー海（Energy Sea）：背景媒質。弾性的な戻りと指向応答を与えます。
• 張力／指向テクスチャ：媒質が受ける引っ張りの向きと強さ。
• 位相ロック：位相関係が噛み合い、安定した拍節を保ちます。
• 近傍／中間／遠方：距離による三層。遠いほど時間平均で平滑化されます。
• 時間平均：観測窓内の速く小さい変動をならし、安定特徴を抽出します。

結び

エネルギー糸理論（EFT）では、電子は環として閉じたエネルギー糸です。近傍では内向きテクスチャが負電荷を定め、中間〜遠方では対称で安定な浅い鉢として質量が現れます。スピンと磁気モーメントは閉循環と拍節の自然な帰結です。環ドーナツ → 柔らかな縁の枕 → 対称な浅い鉢という連続図は、近・中・遠の外観を一体化し、明確な境界条件が既存の実験事実との整合を支えます。

図示

読者ガイド

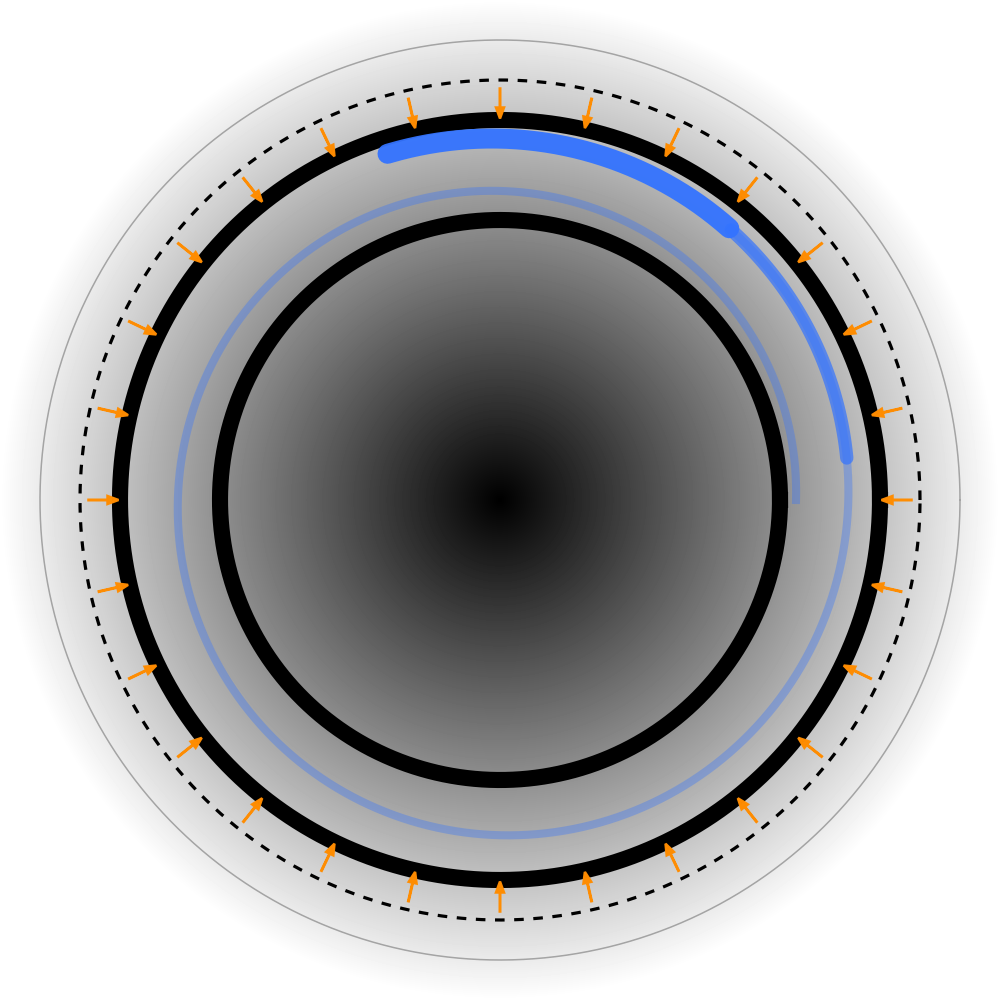
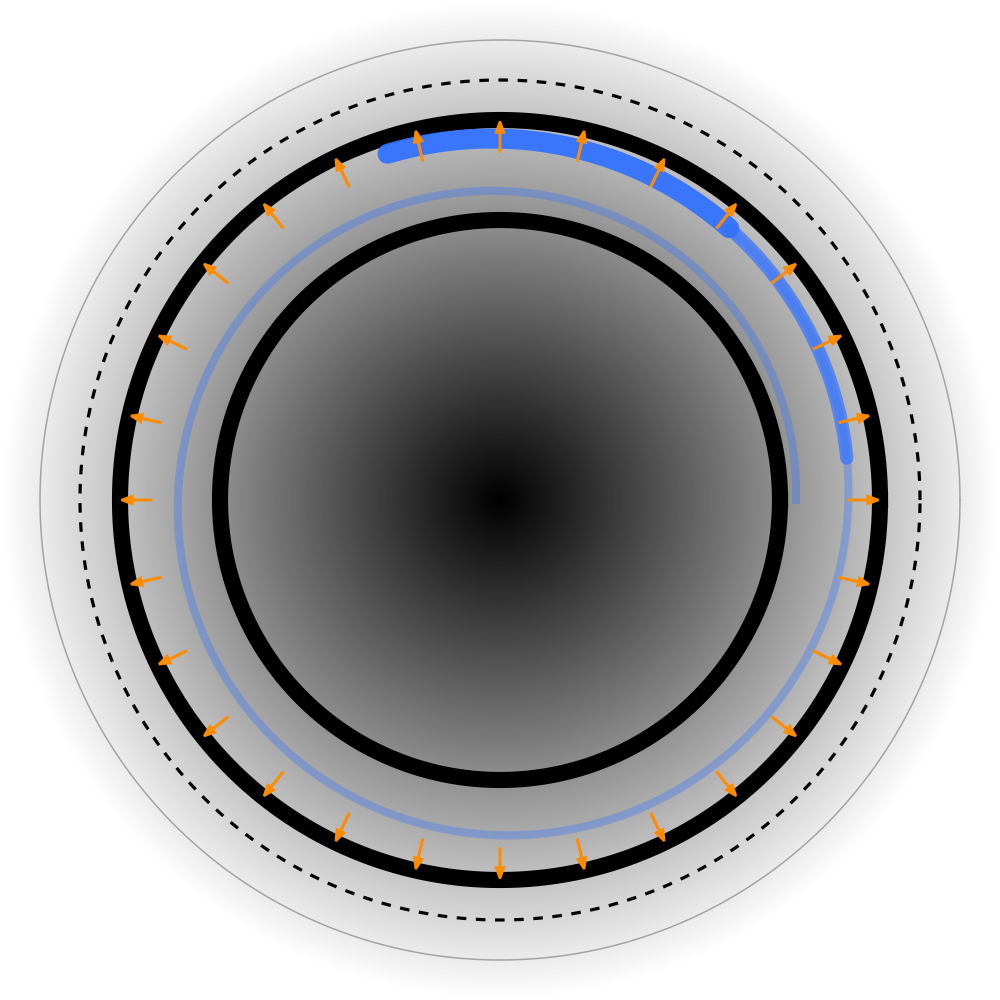
本仕様は、負の電子（図1）と陽電子（図2）の対になる図を描く際の要点をまとめます。目的は、実在の粒子軌道や剛体的な電流ループを想起させることなく、近傍・中間・遠方の各領域における構造をわかりやすく示すことです。

1. I 本体と厚み
   • 単一の閉じた主環：描くのは一本の糸が輪として閉じた構造です。二重の輪郭がある場合は、有限の厚みと自立性を表すだけで、二本の糸を意味しません。初出の用語：エネルギー糸（Energy Threads）、エネルギー海（Energy Sea）。
   • 等価循環／環状通量：磁気モーメントは、観測可能な幾何学的半径に依存しない等価循環に由来します。主環そのものを「電流回路」としては描きません。
2. II 位相カデンツ（軌道ではない／環内の青い螺旋）
   • 青い螺旋状の位相前線：内縁と外縁の間に青い螺旋を描き、瞬間の位相前線とロックされた拍（カデンツ）を示します。
   • 薄い尾部→強い先頭：尾部は細く淡く、先頭は太く濃くして、手性と時間方向を表します。これは位相のタイミング表示であり、粒子の軌跡ではありません。
3. III 近傍の指向テクスチャ（電荷の極性を定義）
   • 放射状の橙色マイクロ矢印：環の周囲に、内向きの短い矢印を帯状に配置します。これは負電荷の近傍テクスチャを符号化します。微視的には、矢印に沿う運動は抵抗が小さく、逆らう運動は大きくなり、引力／斥力の起点になります。
   • 陽電子の鏡像：陽電子の図では矢印を外向きに反転させ、応答の符号が鏡像になることを示します。
4. IV 中間領域の「遷移クッション」
   柔らかな点線の環：近傍の細部をならして束ねる層として描き、より均質な振る舞いへ移る過程を示します。時間平均によって局所的な異方性が徐々に減衰することを伝えます。
5. V 遠方領域の「対称な浅い鉢」
   同心グラデーション／等深リング：中心から縁へ向かう濃淡と細い等深リングで、軸対称の引きを表現します。これは質量の安定した外観に対応します。固定的な双極子の偏りは入れません。
6. VI ラベル用アンカー
   • 環内の青い螺旋状位相前線
   • 近傍の放射状矢印の向き
   • 遷移クッションの外縁
   • 浅い鉢の開口と等深リング
7. VII 付記（読者向け）
   • 「位相バンドが走る」とはモード前線の伝播を指し、物質や情報の超光速伝送を意味しません。
   • 遠方の外観は等方的で、等価原理および現在の観測と整合します。現行のエネルギー域と時間窓では、形状因子は点状外観へ収束する必要があります。