5.7 中性子：『リング織り』の像、直観への手がかり、そして検証

目次 ／ 第5章：微視的粒子

読者ガイド：なぜ「材質レイヤー」の図が役に立つのか

本節は主流理論を置き換えるものではありません。量子色力学は中性子の諸量をよく再現します。ただし像が不足しています。中性なのに磁気モーメントを持つことをどう描くか、平均二乗電荷半径の負符号を数値以上にどう理解するか、自由中性子が速くβ⁻崩壊する一方で核内では安定し得るのはなぜか。電気双極子モーメントの厳しい上限は、電気的な相殺が高対称でなければならないことを示しつつ、磁気モーメントは残る必要があります。さらに、従来図は遠方場や超短時間の高エネルギーに偏りがちで、近傍構造—電気と磁気が同一幾何で結びつく様—は描かれません。そこで**エネルギー糸（Energy Threads, EFT）**は、直観を補うために『リング織り』の像を加え、データ整合を保ちます。

I 中性子の「結び」：多環織りによる電性相殺の設計

• 基本構成：エネルギー海が複数の糸を同時に引き上げ、複数のサブ環が閉じます。結合バンド（高張力チャネル）が相互ロックと張力配平を担い、コンパクトな織りになります。
• 相殺パターン：プロトン同様に多環＋バンドですが、サブ環ごとに断面の偏りを交互に配置します。すなわち外強・内弱の環と内強・外弱の環を織り交ぜ、時間平均で外向きと内向きのテクスチャが相殺され、遠方は電気的に中性になります。バンドは剛壁ではなく、指向と張力の地形に沿って位相・エネルギーのパケット（グルーオン様の交換）が走る帯です。
• 離散性と安定性：ロック数や織りのパリティは離散です。中性化には特定の組合せが必要で、閉環・位相ロック・張力配平・寸法とエネルギーの閾・外部せん断の上限を同時に満たすと安定、外れると解体します。

II 質量の外観：対称な浅い鉢と「わずかにプロトンより重い」の直観

• 張力地形：中性子をエネルギー海に置くと、対称で浅い鉢が刻まれ、深さ・口径はプロトンと近い値になります。環とバンドがこれを安定かつ等方に保ちます。
• なぜ質量か：中性子を動かすと鉢と媒質を伴って動き、結合が強いほど鉢は深く安定して慣性が増します。プロトンに比べ、電気相殺の実装にわずかな構造コストが要るため、質量が少し大きい直観に結びつきます（数値は測定に従います）。

III 電荷の外観：近傍に構造、遠方はゼロ／負符号半径の由来

電場は張力勾配の半径方向の延長、磁場は並進または内部循環による方位方向の巻き返しです。

• 近傍：相反する偏りが外向きと内向きのテクスチャを冠域に刻み、近傍は非ゼロで構造的です。
• 中〜遠方：多環相殺と時間平均で平滑化が進み、遠方には等方な質量鉢のみが残って電荷はゼロになります。
• なぜ平均二乗半径が負か（定性的）：近傍では負側の成分がやや縁寄り、正側の成分がやや内側に寄ります。半径重み付き平均では二乗平均が負になります。これは形状因子や半径拘束を変えず、「なぜ負か」の直観を与えます。

IV スピンと磁気モーメント：電気的中性 ≠ 非磁性

• 協調する閉流からのスピン：位相カデンツをもつ多環循環の合成でスピン1/2が立ち上がります。
• 磁気モーメントの符号と大きさ：電気テクスチャが相殺しても、等価循環／トーラス・フラックスは非ゼロになり得ます。支配的な手性と重みがスピンと逆符号のモーメントとその大きさを定めます。外強・内強の配分に感度がありますが、測定値と一致することが条件です（EFTのハードコミット）。
• 歳差と EDM：外部の指向ドメインを変えると、較正可能な準位シフトを伴う歳差が現れます。ほぼゼロの電気双極子モーメントは高対称な相殺の結果で、制御された張力勾配下では微小で線形・可逆・較正可能な応答のみを許容します。

V 三つの重ね図：多環ドーナツ → 細縁クッション → 軸対称の浅い鉢

• 近景：多環ドーナツ。有限厚の環に青い位相前線、サブ環の一部は外強、一部は内強で、近傍テクスチャが明瞭です。
• 中景：細縁クッション。近傍の細部を平滑化し、外向き／内向きの偏りは打ち消されます。
• 遠景：軸対称の浅い鉢。質量外観は安定で等方、電気外観は消え、鉢によるガイドのみ残ります。

VI スケールと観測可能性：内側は複合、外側は横からプロファイル可能

• 多層コア：コアは極めてコンパクトで直接像では分解困難。高エネルギー・短時間の散乱はほぼ点状の形状因子を返します。
• 電荷半径と偏光：弾性・偏光散乱は負の平均二乗半径と非常に弱い偏光を読み出し、「縁で負／内で正」の直観と整合します。
• 滑らかな遷移：近から遠へ連続的にならされ、遠方には鉢だけが見え、相殺の微細模様は見えません。

VII 生成と変換：β⁻崩壊の材質的な描写

• 生成：高張力・高密度事象で複数糸が立ち上がり、環が閉じてバンドでロックされ、相殺による中性が固定されます。
• 変換（自由β⁻）：せん断や内部ミスマッチで最適相殺が崩れると、再ロックと再結合が低コスト経路になります。あるサブ環群は外強優位のプロトン織りに再配置され、別の群は再結合チャネルに沿って電子を核化し、位相・運動量差は反ニュートリノのパケットとして運び去られます。巨視的にはβ⁻崩壊であり、電荷・エネルギー・運動量・バリオン／レプトン数の保存は厳密に満たされます。

VIII 現代理論との照合：一致と付加価値

1. 一致：
   • スピン–モーメントの対：スピン1/2と負符号で非ゼロの磁気モーメント。歳差の則は主流と合致。
   • 半径と形状因子：遠方の電荷はゼロ。負符号は「縁で負／内で正」の配置で説明可能。弾性／偏光の拘束は維持。
   • ほぼ点状散乱：コンパクトなコアと時間平均が高エネルギー応答を説明。
2. 付加価値：
   • 中性の幾何：外貼りのラベルではなく、サブ環の幾何学的相殺として実現。
   • βの幾何学的ストーリー：再結合＋核化で「中性子 → 陽子＋電子＋反ニュートリノ」を視覚的に理解。
   • 電磁の統一像：電気＝テクスチャの半径延長、磁気＝並進／自転による方位巻き返し。共通の近傍幾何と時間窓で結ばれます。
3. 整合性と境界（要点）：遠方の正味電荷0、負符号の半径は形状因子と整合。新たな測定半径は導入しません。スピン1/2維持、磁気モーメントは負で測定範囲内、環境由来の微小ずれは可逆・再現・較正可能。高Q²ではDISへ収束、追加の角度パターンやスケールは不要。EDMは均質環境でほぼゼロ、張力勾配下では微小・線形・可逆の応答のみ。偏極率や散乱の既存値も不変です。

IX データの読み方：像面／偏光／時間／スペクトル

• 像面：全体の電気相殺の中で縁の弱いネガティブ強調を探します。
• 偏光：「縁で負／内で正」と整合する弱いバンドや位相差を確認します。
• 時間：閾値を越えると再結合エコーが短く現れ、スケールはバンド強度とロックのコヒーレンスに従います。
• スペクトル：再処理環境ではソフト域の穏やかな持ち上がりと極小の分裂が見られ、二重相殺に由来し、振幅はバックグラウンドとロック強度で決まります。

X 近・中距離に向けた予測と検証

• 近傍キラル散乱の「相殺フィンガープリント」：
  予測：軌道角運動量をもつプローブは縁で負／内で正に一致する位相対称を示し、陽子／電子に対して符号が補完関係になります。
• 半径符号のイメージング：
  予測：エネルギーを跨いだ弾性／偏光形状因子の比較で負のプロファイルが安定に得られ、遠方の電気外観はゼロのままです。
• 勾配下の磁気モーメント微小ドリフト：
  予測：張力勾配下でモーメントは線形・可逆・較正可能に漂い、その傾きは陽子と系統的に異なります。
• β変換の幾何学的相伴：
  予測：再結合を触発するパルス下で、プロトン様成分の増加と電子パケットの核化が同時に現れ、反ニュートリノ・パケットとの時間相関が弱く読み取れます。

要するに：中性とは「構造化された相殺」である

中性子は多本の糸から成る閉じた織りです。サブ環が外強と内強を交互に担い、電気テクスチャを相殺して中性を固定します。質量の鉢が遠方の安定・等方を与えます。協調する閉循環と位相カデンツがスピン1/2と負符号で非ゼロの磁気モーメントを生みます。真空でのβ⁻は「再結合–核化」のエピソードです。多環ドーナツ（近）→ 細縁クッション（中）→ 軸対称の浅い鉢（遠）という三枚で、データ整合かつ検証可能な一枚絵が立ち上がります。中性は無ではなく、構造化された相殺であり、質量・電性・磁性・崩壊が同一幾何に貫かれているのです。

図示

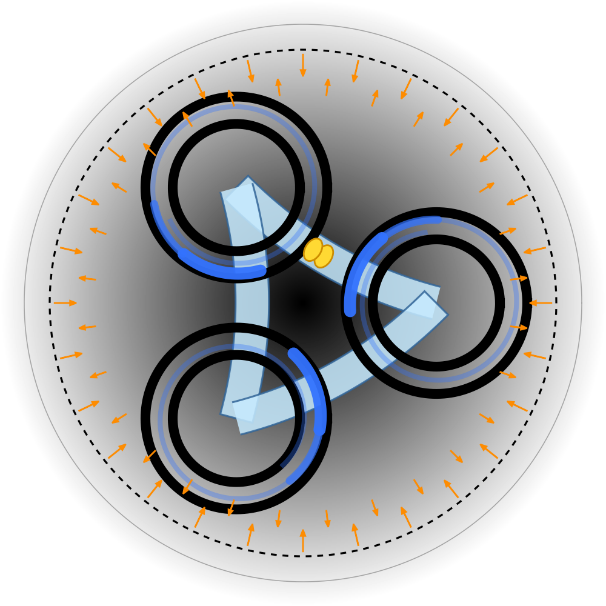
1. I 本体と厚み
   • 相互ロックする主環群：複数のエネルギー糸がそれぞれ環として閉じ、結合機構でロックされて緻密な織りを成します。各主環は二重実線で描き、有限の厚みと自立性を示します（複数糸の寄せ集めではありません）。
   • 等価循環／トーラス・フラックス：中性子の磁気モーメントは等価循環／環状通量の合成に由来し、観測可能な幾何学半径に依存しません（いわゆる「電流ループ」直観ではありません）。
2. II 色フラックス・チューブの可視化規約
   • 意味：物理的な管ではなく、エネルギー海の指向と張力が高張の通路として伸びた拘束ポテンシャルの帯です。
   • なぜ弧帯か：張りが強く、流路抵抗が小さい部位を強調するためです。色や帯幅は可視コーディングで、壁材を意味しません。
   • 対応：QCD の色フラックス束に相当します。高エネルギー・短時間窓では解釈がパートン像へ収束し、新たな「構造半径」は導入しません。
   • 図の要：淡青の弧帯三本が主環を結び、位相ロック＋張力配平の拘束チャネルを示します。
3. III グルーオンの可視化規約
   • 意味：局在した位相・エネルギーのパケットが高張チャネルを伝わる１回限りの交換／再結合事象であり、安定な小球ではありません。
   • アイコンの理由：**黄色の「ピーナツ形」**は事象の所在を知らせる記号です。長軸をチャネル接線方向に置き、チャネル沿いの輸送を示します。
   • 対応：グルーオン場の量子励起／交換に対応し、観測量と整合します。
4. IV 位相カデンツ（軌跡ではない）
   • 青い螺旋状の位相前線：各主環の内縁と外縁の間に描き、ロックした拍と手性を示します。先端は強く、後ろは徐々にフェードアウトします。
   • 注意：「走る位相バンド」はモード前線の移動を指し、物質や情報の超光速輸送を意味しません。
5. V 近傍の指向テクスチャ（電気的相殺）
   • 橙色の二重クラウン矢印帯：
     1. 外側クラウンは内向き（負極性の寄与、縁に近い）。
     2. 内側クラウンは外向き（正極性の寄与、より内側）。
     3. 二つのクラウンを角度ずらしで配置し、時間平均で外向き／内向きテクスチャが相殺され、遠方の電気外観はゼロになります。
   • 直観の糸口：この**「縁で負／内で正」**という重み付けは、平均二乗電荷半径の負符号を与える幾何学的手がかりになります（数値は参照データに準拠）。
6. VI 中間領域の「遷移クッション」
   • 点線リング：近傍のマイクロテクスチャを時間平均の等方へ滑らかに移し替え、中性の顕在化を図る視覚補助です。
   • 数値メモ：この見せ方は測定済みの形状因子や電荷半径を変更しません。直観整理のための表示です。
7. VII 遠方領域の「対称で浅い鉢」
   • 同心グラデーション＋等深リング：軸対称の浅い鉢（安定した質量の外観）を描き、固定双極子の偏心は持ち込みません。
   • 細い参照リング：遠方の細い実線リングは読み取り・スケールの基準で、物理境界ではありません。グラデーションは枠まで延ばせますが、読み取りは細リング基準です。
8. VIII ラベル用アンカー
   • 青い螺旋位相前線（各主環内）
   • 淡青のフラックス弧帯（三本・高張チャネル）
   • 黄色のグルーオン記号（チャネル接線上）
   • 橙色二重クラウン矢印帯（外クラウン内向き／内クラウン外向き）
   • 遷移クッション外縁（点線リング）
   • 遠方の細い参照リングと同心グラデーション
9. IX 境界注（キャプション相当）
   • 点状極限：高エネルギー／短時間では形状因子が点状応答に収束します。本図は新たな構造半径を仮定しません。
   • 可視化 ≠ 新数値：「縁で負／内で正」「チャネル」「パケット」は視覚言語であり、既存の形状因子・半径・パートン分布を変更しません。
   • 磁気モーメントの起源：等価循環／環状通量に由来します。環境に依存する微小ずれは可逆・再現・較正可能である必要があります。