5.9 クォークのファミリー

目次 ／ 第5章：微視的粒子

ひとことで:
エネルギー・スレッド理論（EFT）では、クォークは点ではなく、「極小のスレッド核」と「色チャネル」から成る開放型ユニットとして描かれます。核は非常に短く密な結び目で、キラリティを定め、スピンと自己支持エネルギーの一部を担います。色チャネルはエネルギーの海（Energy Sea）から引き出された高張力の回廊であり、実体の管や第 2 のスレッドではありません。ほかのクォークと結合してエネルギー収支が閉じたときにのみ安定化します。このため、長寿命なのは全体として無色の複合体（メソン、バリオン、グルーオンに富む束縛状態）であり、単独のクォークは巨視的には分離できません。以後は略称を避け、エネルギー・スレッド理論という表記を用います。

I. 最小の物理像：核＋色チャネル（3 色＝相互に置換可能な 3 本の経路）

• スレッド核
  **エネルギー・スレッド（Energy Threads）**がエネルギーの海内でつくる微小な結び目です。キラリティを定め、スピンと慣性（自己支持エネルギー）に寄与します。フレーバー（up, down, strange, charm, bottom, top）の違いは、巻き付けの階数や位相モードの違いとして理解できます。
• 色チャネル（色スレッド回廊）
  抜き出されるのはスレッド本体ではなく、核の「色ポート」が海の中に張力回廊を励起します。「色」は独立だが相互に置換可能な 3 本の指向経路を指します。
  閉じ方の向き付け：複合体において 3 本の指向ベクトルの和がゼロ（無色）になると、遠方場が封じられ、構造は安定します。

補足：色回廊は実体物ではなく、張力をもった空間的な指向バンドです。グルーオンは、この回廊を伝わる位相・エネルギーのパケットであり、交換や再結合の事象として現れます。小さな球ではありません。

II. 禁閉の具体像：単独クォークが見えない理由

引き離された 2 個のクォークは、高張力の回廊でつながっていると考えます。

• 引くほどコストが増える：回廊の張力はほぼ一定なので、エネルギーは距離に対してほぼ線形に増大します。
• より安い出口：しきい値を超えると、エネルギーの海が中央付近で再結合し、クォーク–反クォーク対（q–q̄）を成核します。長い回廊は2 本の短い回廊に切り分けられ、それぞれがメソンとして閉じます。

結論：観測されるのはジェットや「メソンの雨」であって、単独のクォークを引き抜く現象ではありません。

III. ハドロンの組み上がり：メソン、バリオン、そして Y 形閉鎖

• メソン（q + q̄）
  ほぼ直線の色回廊が 2 つの核をドッキングし、全体が無色になります。
• バリオン（q + q + q）
  3 本の色回廊が空間内のY ジャンクションに収束します。これは三角形の周回より低コストです。3 本の指向ベクトルの和はゼロとなり、構造が閉じます。
• グルーオン交換
  位相／フラックスのパケットが回廊内を走り、3 本の経路間で占有を受け渡します。これが色の交換として現れます。

IV. フレーバー（up, down, strange, charm, bottom, top）：巻き付け階数と寿命

• 巻き付けの階数やモードが高いほど成核コストが大きく、粒子は重くかつ短命になります。より低い階数へ崩壊しやすくなります。
• トップ・クォークは非常に重く、極めて速く崩壊するため、しばしばハドロン化が間に合いません。観測と整合的です。

V. 質量・電荷・スピン：勘定の内訳

1. 質量（2 つの勘定）
   • 核の自己支持エネルギー（曲げ／ねじれ）。
   • 色回廊に蓄えられる張力エネルギー（回廊の「エネルギー在庫」）。
     これにより「陽子質量の大半は強い相互作用に由来する」という言明が具体化します。細い回廊の張力は、クォークの「裸質量」を大きく上回ります。
2. 電荷（1/3 の倍数になる理由）
   クォークの電磁的な見かけは、核の近傍場における指向性分極から生じます。この指向性の予算の一部が色回廊に食われるため、電磁的な投影は分数になります。up 族は多め（+2/3）、down 族は少なめ（−1/3）。
   数値の整合：電荷の値は厳密に ±1/3、±2/3 に一致します。ここでは像の与え方を説明するだけで、数値は変更しません。
3. スピン（誰がどれだけ寄与するか）
   核の全体ねじれと、回廊内のねじれ波・グルーオン角運動量が合わさって有効スピンを与えます。ハドロン内部での配分は系ごとに異なり、クォーク・スピンが全体の一部に過ぎないという実験的な分解を説明します。

VI. スケール依存のふるまい：短距離でほぼ自由、長距離で強く拘束

• 極短距離（高 Q²）
  核同士が近づくと回廊の断面が広がり、インピーダンスが低下します。交換は**「広帯域トンネル」のようになり、クォークはほぼ自由**（漸近的自由）に見えます。
• 引き離し（低 Q²）
  回廊は細く強くなり、エネルギーは距離にほぼ比例して増えます。系は切断して対生成へ向かい、閉じたハドロンに戻ります（禁閉）。

このように、漸近的自由と禁閉は同一のエネルギー勘定の両側面です。

VII. 標準模型との対応（対立ではなく用語の橋渡し）

• 3 色 ↔ 3 本の指向回廊（色経路の幾何学的可視化）
• グルーオン ↔ 回廊を走る位相／フラックスのパケット（占有の受け渡し）。球ではない
• 禁閉とジェット ↔ 距離に対する線形のエネルギー増加＋再結合による対生成
• ハドロン内部 ↔ 直線回廊で閉じるメソン、Y ジャンクションで閉じるバリオン
• 質量の主因は強い相互作用 ↔ 回廊張力＋核の自己支持エネルギーが優勢
• 分数電荷 ↔ 近傍場の分極の電磁投影（色回廊による消費の後）
• トップがハドロン化しにくい ↔ 成核時間が崩壊時間を上回る

VIII. 境界条件（既存データと整合する要点）

• 深非弾性散乱（DIS）とパートン像
  高 Q²・DIS では記述がパートン視へ収束します。既存のパートン分布関数（PDF）とスケーリング則は保持されます。
• 電磁的一貫性
  電荷は ±1/3、±2/3 に据え置きです。形状因子とそのエネルギー依存性は測定と整合します。
• 分光とハドロン化
  共鳴スペクトル、ジェット位相空間、フラグメンテーション関数は誤差帯に収まります。「線形ポテンシャル＋対生成による切断」という直感的表現が偽のピークを導入してはなりません。
• 保存則と力学的安定
  色、フレーバー、エネルギー、運動量、角運動量、バリオン数の保存は厳密に満たされます。原因と結果の逆転や自己増幅的不安定はありません。
• 可視化 ≠ 数値変更
  回廊／パケット／Y ジャンクションといった比喩は直感の翻訳であり、パラメータやフィットは変更しません。

要するに
クォークはスレッド核と色チャネルから成ります。色チャネルはエネルギーの海から引き出された高張力の経路で、複数の核を無色の全体へとロックします。引けば引くほどコストが増え、最終的に再結合が対生成を起こし、系は閉じたハドロンへ戻ります。したがって私たちが観測するのはジェットとハドロンであり、単独クォークではありません。質量、スピン、分数電荷も、この具体的マップの中で自然な位置を占めます。

図示

1. 単一クォーク・ユニット（核＋生まれつつある回廊）

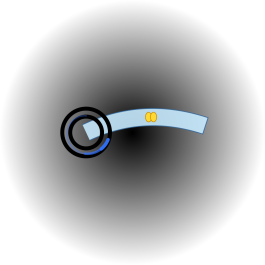
• ポイント：単体のクォークは開放であり、安定には他とのドッキングが要る。
• 読み取りの錨：二重環＝核、淡色弧＝色回廊、黄色＝グルーオン・パケット、灰の勾配＝浅いベイスン。
• グルーオン：回廊上の**「ピーナッツ」形の黄色いパケット**は、位相・エネルギーのパケット（交換／再結合の 1 事象）を表す。球ではない。
• 位相前線：核上の濃い青の弧（先端を太く）で位相ロックを示す。
• 本体：左に核（二重環で描かれた自立的な中心）、右へ伸びる淡色の弧が色回廊（張力バンド、実体の管ではない）。

2. メソン（q + q̄：直線回廊で閉鎖）

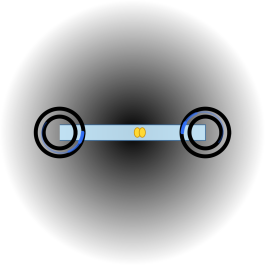
• ポイント：メソンは**「一本の直線回廊」**が両端で閉じた姿。
• 錨：端の二重環＝q と q̄ の核、中央の淡帯＝回廊、黄色パケット＝グルーオン。電荷の矢印なし（無色）。
• 位相前線：両端に青の弧、中央の黄色パケットが色交換を示す。
• 本体：左右に 1 個ずつの核、それらをほぼ直線の回廊が接続。全体は無色。

3. バリオン（§§ 5.6 陽子・5.7 中性子）
   3 個のクォーク、3 本の回廊が中央のY ジャンクションに集合。核の二重線、青の位相弧、「移行クッション」、遠方場の細線、同心グラデーションなど、他のレイヤも同じ記法で表す。