5.12 原子（離散的なエネルギー準位・遷移・統計的制約）

目次 ／ 第5章：微視的粒子

I. イントロダクションと目的
本節では、一般読者にも読みやすい形で次の三点を説明します。

• 離散的なエネルギー準位：原子内の電子が、なぜごく限られた殻や形だけにとどまり、任意のエネルギーを取らないのか。
• 遷移とスペクトル：電子が準位のあいだをどのように移り、その差分エネルギーを光として「清算」するのか。なぜスペクトル線が離散的で強弱があるのか。
• 統計的制約：単独占有と対占有の意味、同一状態を二つの電子が同時に占められない理由、フントの規則の働き、そしてこれらが**エネルギー糸理論（EFT）**でどのような物質的イメージを持つのか。

数式は使わず、必要に応じて教室と座席、確率雲といった比喩を用います。n、l、m、ΔE、Δl は記号ラベルとして示します。

II. 教科書的な基準線（比較のため）

• 原子核はクーロンポテンシャルを与え、電子は境界条件と対称性を満たす量子状態を占有します。
• 許される状態は主量子数 n、軌道角運動量 l、磁気量子数 m、スピンで標識され、s/p/d/f は l = 0/1/2/3 に対応します。
• 同一原子の電子はフェルミ–ディラック統計とパウリの排他原理に従い、同じ量子状態には反平行スピンの二個までしか入れません。
• 遷移は選択則（典型例は Δl = ±1）に従い、エネルギー差 ΔE は光子として出入りします。線の強度は遷移行列要素、線幅は自然幅・ドップラー効果・衝突・外部場などで決まります。

以上は実証的に確立した枠組みです。本節ではこれを土台に、**エネルギー糸理論（EFT）**による統一的で物質感のある直観像を提示します。その後は「エネルギー糸理論」と記します。

III. エネルギー糸理論における中核像：浅い張力の“盆地”と閉ループの立相チャネル

1. エネルギーの海（Energy Sea）：真空を物性をもつ媒質として捉えます。その局所的な「かたさ」は**張力（Tension）**を定め、伝播の上限や抵抗・ガイドの基準スケールになります。
2. 浅い張力盆地：原子核がこの海に、ほぼ球対称の浅い「盆地」を押し込みます。遠くからは質量とガイドの見かけ、近くでは電子の安定状態を縁取る「地形」になります。
3. 電子は閉じた糸の輪：電子は点ではなく、エネルギーの糸（Energy Threads）からなる自己維持的な閉ループです。拡がらずに長く留まるには、周囲の張力地形がつくる立相（定常位相）のチャネルに、自身の位相リズムをロックする必要があります。
4. 立相チャネル＝許される準位と形：
   • s チャネル：ほぼ球状の「リングベルト状の確率雲」。
   • p チャネル：互いに直交する三組の「ダンベル形の確率雲」。
   • d/f チャネル：より複雑で指向性のある幾何。
5. 要点：離散準位とは「盆地内で位相が閉じ、かつ最も省エネでいられる通り道」の集合です。数が限られるため離散になります。

IV. 準位が離散になる理由（エネルギー糸理論の直観）

• 境界と省エネ：糸が自立するには、内部リズムと盆地の復元的な引き戻しを釣り合わせ、安定ループを作る必要があります。位相を閉じつつエネルギーも小さくできる幾何とリズムの組は少数で、それが n・l・m による離散的な「座標」に対応します。
• 形は地形が選ぶ：球対称の盆地は s を優先し、角運動量が必要なときには二葉の p が「生え」、さらに上で d/f になります。形は単なるラベルではなく、地形・位相閉合・エネルギーコストの折衷結果です。
• 階層性：外側のチャネルほど広く拘束が緩い一方、撹乱に弱くなります。したがって励起が大きい（n が大きい）状態ほど電離しやすくなります。

V. 統計的制約：単独占有・対占有と「同じところに二つは入らない」

1. 排他原理の物質的説明：
   二本のループが同相のまま同じチャネルを共有すると、近傍では張力せん断が衝突してエネルギー消費が急増し、構造は維持できません。解は二つです。
   • 別のチャネルへ散らす（まず単独占有を優先）。
   • 同じチャネルで位相を補い合う（反平行スピンのペア）。一つの確率雲を致命的なせん断なく共有でき、これが対占有です。
2. 空・単独・対：
   • 空：そのチャネルを占める糸がない。
   • 単独：一本だけで最も安定。
   • 対：位相が補完的な二本が共存。安定だが、別々の単独二つよりわずかに高エネルギー。
3. フントの規則の物質像：
   三重縮退の集合（pₓ/pᵧ/p𝓏）では、糸はまず単独で異なる向きに分散し、近傍のせん断を分担して全エネルギーを下げます。やむを得ないときのみ同じ向きで対を作ります。こうして「一状態に最大二つ」「まず単独、次に対」という規則が、張力せん断のしきいと位相補完という具体的尺度から導かれます。

VI. 遷移：電子が光として「精算」するしくみ

1. トリガー：外部からの供給（加熱・衝突・光ポンピング）や内部再配分で、糸が低エネルギーのチャネルから高エネルギー側へ持ち上がります。励起チャネルは長く保てず、有限の滞在後により省エネなチャネルへ戻ります。
2. エネルギーの行き先：チャネル変更で生じた余剰や不足は、エネルギーの海に撹乱パケットとして出入りし、巨視的には光になります。
   • 放出：高→低でパケットを放つ（発光線）。
   • 吸収：低→高でチャネル差に合うパケットを吸う（吸収線）。
3. 線が離散になる理由：選べるチャネルが離散であるため、ΔE も限られた差だけを取り、周波数は少数の段に並びます。
4. 選択則の直観：チャネル間の移動には形とキラリティの適合が必要で、角運動量と向きの収支を海と合わせます。
   • 典型的な Δl = ±1 は、「雲の形の等級」を一段変えることで、エネルギー・角運動量・結合効率のつり合いが取れることを示します。
   • Δm のパターンは、外部の指向場（印加場・偏光など）への結合幾何で決まります。
5. 線強度を決めるもの：位相重なりの面積と結合の抵抗が二本柱です。
   • 重なり大・抵抗小 → 振動子強度が大きく線は明るい。
   • 重なり小・抵抗大 → 禁制あるいは弱い遷移となり、線は弱いか見えません。

VII. 線形と環境：同じ線が広がる・ずれる・分裂する理由

• 自然幅：励起状態の有限寿命により、各チャネルには固有の「窓」が生じ、自然広がりとなります。
• 熱運動（ドップラー）：原子全体の運動が放出パケットの周波数をわずかにずらし、ガウス型の広がりが重なります。
• 衝突（圧力広がり）：近傍からの繰り返しの「圧し・緩め」で位相が揺らぎ、線形が広がります。
• 外部場（シュタルク／ゼーマン）：指向場が立相チャネルの縁を再構成し、縮退をゆるやかに解くことで、予測可能な分裂とシフトが現れます。
• ひと言で：線形＝チャネル固有の窓 ＋ 周囲の張力と指向場による「ジッター・再スケール・分裂」。

VIII. なぜ環境張力が高いほど → 内部振動が遅くなる → 発光周波数が下がるのか

• 「張力が高い」とは何か、そのとき区別すべき二つの量
  a) 状況. ここでいう環境張力が高いとは、浅い「盆地」がより剛直な環境に置かれることです（重力ポテンシャルの増大、圧縮や密度の上昇、強い配向場など）。その結果、エネルギーの海（Energy Sea）は一層強く張られます。
  b) 二つの量. 伝播上限は「その媒質が支えられる最速応答」、定常位相の周波数は「環境負荷を受ける束縛モードの拍（ケイデンス）」です。
  c) 同一ではない. 伝播上限が上がっても、束縛振動子は環境による引きずりで遅くなる場合があります。
• エネルギー糸理論（EFT）における三つの合成効果
  a) 盆地が深く広くなる → 周回が長くなる（幾何学的遅延）. 張力の上昇は盆地を深く広げ、安定チャネルの等位相面を外側へ押し出します。同じチャネルでも一拍ごとの閉じた経路が長くなり、一周に要する時間が延びます。
  b) より多くの媒質を「巻き込む」 → 実効慣性が増す（リアクティブ負荷）. 張力が高いほど近傍場の結合が強まり、位相を一度回すたびに厚い媒質層を一緒に揺らします。この層は付加質量のように働き、固有の拍を遅くします（ばね‐質量系は「より粘い」流体中では遅く振動します）。
  c) 反響の再結合 → 位相遅れ（非局所遅延）. 高張力では、糸の近傍が励起した微擾が盆地内で反響しやすく、本体へ戻ってきます。各拍に反響由来の位相遅れが加わり、位相閉合がより遅れて満たされます。言い換えると、各拍で媒質に蓄え／取り出すリアクティブエネルギーが増えるため、拍が伸びます。
• 合成結果
  a) 同一の原子・同一チャネルでも、束縛モードの固有周波数は全体に低下します。
  b) 準位間隔も縮み、しばしば近似的に同一スケールでスライドします。
  c) そのため隣接準位の ΔE が小さくなり、発光／吸収線は**低周波側（赤側）**へ移動します。
• 補足説明
  a) 「張力が高いと伝播は速くならないのか」 自由波の上限としては速くなり得ます。しかし束縛振動子の拍は 幾何 + 付加質量 + 反響遅れ で決まり、後二者が勝って遅くなります。
  b) 「重力赤方偏移と同じか」 EFT では、重力ポテンシャルの増大は張力の上昇に対応します。上の三機構で原子の「局所時計」が遅れ、線は赤側へ移動します。観測像としては一般相対論の赤方偏移と一致しますが、EFT は媒質結合と幾何に基づく物質的な経路を与えます。
  c) 上限と拍の違い. 自由波の上限が速くても、束縛モードの拍が速くなるとは限りません。負荷と遅延がテンポを決めます。
• 直観的で検証可能な手がかり
  a) 同一核・異なる環境. 白色矮星の表面近くでは、実験室よりも原子線が赤側に寄ります。実験室でも、圧力／密度／配向の上昇に伴い、標準的な Stark／Zeeman および圧力広がりを差し引いた後で、線中心に繰り返し再現される微小な赤側シフトが見られます。
  b) 同位体／等構造系. 巻き込まれやすい（高い分極率、近傍場が「軟らかい」）系ほど、同一の環境張力で中心周波数の低下がより顕著になります。

IX. 電子が「雲」のように見え、あたかも「さまよう」理由

EFT では、電子は核を回る小球ではなく、エネルギーの糸（Energy Threads）から成る閉じたループです。核が作る張力の浅い盆地に刻まれた少数の定常位相チャネルの内部でのみ長期安定に存在します。「雲」は、その許されたチャネル内での出現確率にほかなりません。電子を狭い領域へ無理に押し込むと近傍場に張力せん断が生じ、同時に位相閉合を維持するため運動量（向きと大きさ）が広がらざるを得ず、エネルギー代償が大きくなります。結果として、安定解は有限の幅をもつ――これが「不確定さ」の物理的な底です。

さらに、エネルギーの海には張力バックグラウンド雑音（TBN）があり、電子ループの位相拍を微弱ながら持続的に揺さぶります。これによりチャネル内部で微細な位相ウォークが生じます。チャネル境界の外側では位相閉合が崩れ、破壊的な自己干渉が振幅を抑え、濃淡が交互に現れる雲模様を残します。測定により電子を局在化すると近傍場はいったん強く締まり、その後は許された定常位相パターンへと戻ります。統計的に見れば、電子は糸＋エネルギーの海＋境界条件によって選び出された安定分布として、許容域の中を「さまよう雲」のようにふるまいます。さまよいは、定常位相の拘束と、つねに存在する背景擾乱が駆動します。

X. まとめ

• 離散準位： 核の張力盆地の中で位相を閉じ、エネルギーを最小にできる少数の定常位相チャネル。
• 統計的制約： 同位相せん断が閾値を超えると二重占有は破綻。位相補完での対占有は安定。フントの規則は、全せん断を最小化する「まず分散、のちに対」の戦略に対応。
• 遷移とスペクトル： チャネルの入れ替えでエネルギーは擾乱パケットとして精算 → 離散スペクトル線。線強度は雲の重なりと結合の抵抗で決まります。
• 環境 → 拍が遅くなる → 周波数が下がる： 長い経路（幾何遅延）＋付加質量（リアクティブ負荷）＋反響遅れ（非局所）が協調して束縛周波数を下げ、間隔を縮め、線を赤側へ移動させます。重力赤方偏移と観測上整合し、物質的な描像を与えます。

四つの典型的な原子（電子を含む）— 概略図

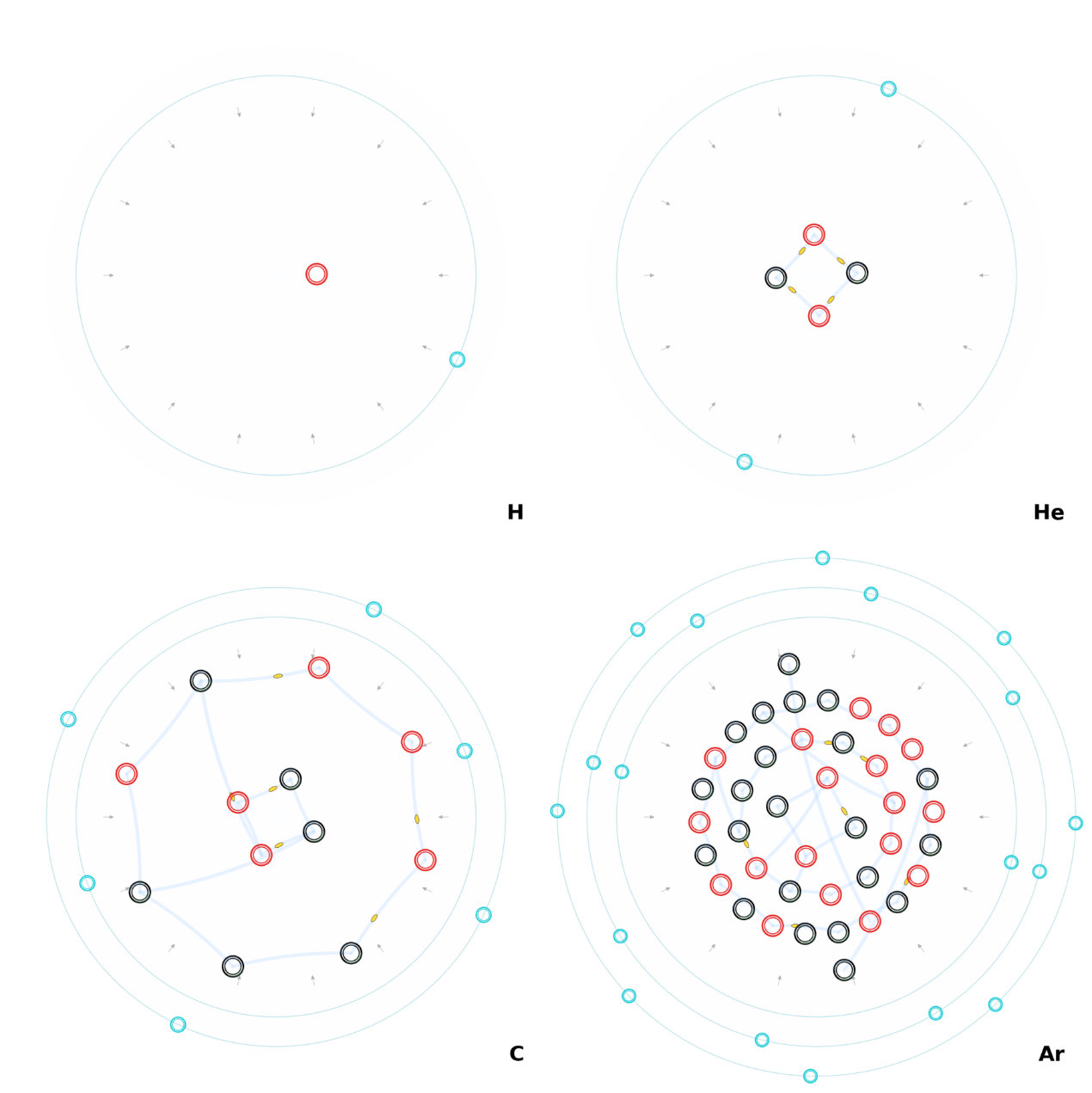
• 核子： 赤いリング＝陽子、黒いリング＝中性子。
• 「色の糸」チューブ： 核子間を結ぶ半透明の青い帯（核子をまたぐ張力の束縛帯）。小さな黄色の楕円はグルーオン様の外観を示唆。
• 電子： 離散的な電子殻上に分布するシアンのミニループ（淡いシアンの同心円）。
• ラベル： 右下の白地に元素の英語略号（H, He, C, Ar など）。
• 同位体と殻： 代表的な同位体（H-1, He-4, C-12, Ar-40）を採用。主殻の集合 [2, 8, 18, 32] で殻構成を示す（例：Ar = [2, 8, 8]）。