5.13 波束（ボソンと重力波）

目次 ／ 第5章：微視的粒子

I. 導入 — 「波束」とは何か
エネルギーの海は、張ったり緩んだりする連続媒質と考えられます。かすかな擾乱が加わると、位相がそろった振動を包む有限の包絡が生まれます。これが波束です。エネルギーの糸（Energy Threads）の安定した結び目として長寿命で自立する粒子とは異なり、波束は自己維持をせず、吸収・散乱・再処理で次第に薄れます。前へ進めるのは、媒質が小領域ごとに状態を隣へ受け渡す「リレー」を行うからです。

II. 波束の伝搬（基本メカニズム）

• 速度は張力が決めます。 張りが強いほどリレーが速くなります。同じ種類の波束でも場所により上限速度が異なり、ほぼ一様な領域では等速のように見えます。
• 経路は勾配が導きます。 抵抗が小さく「滑らか」な方向へ漂いやすく、巨視的には「力を受ける」と表現されます。
• 形はコヒーレンスが支えます。 包絡が締まり、振動が同相であるほど「かたまり」としての振る舞いが明瞭です。コヒーレンスを失うと背景雑音に溶け込みます。
• 環境との双方向作用。 進行中、波束はその場の張力分布を書き換え、環境側も波束を再整形します（減衰、帯域の組み替え、偏光回転など）。

III. なぜ「ボソン」は波束なのか
エネルギー糸理論（EFT）では、ボソンは独立した「粒子種」ではありません。起こり方・走れる場・結合できる相手の違いによって分かれる波束のファミリーです。

1. 光子 — 横せん断型の波束
   • 性質：エネルギーの海に生じる横方向のしわ。偏光を運べます。
   • 到達距離：透明窓では非常に長距離。張力の不均一により、経路の遅延や偏光回転が生じます。
   • 結合：電荷をもつ構造（例：電子近傍の配向）と強く結合します。
   • 観測：干渉・回折・偏光、重力レンズ、時間遅延の「無色散な共通項」。
2. グルーオン — 「色チャネル」に閉じ込められたしわ
   • 性質：色糸束の内部を伝わるエネルギーのうねり。外へ出ると速やかにハドロン片へ「編み戻し」ます。
   • 到達距離：チャネル内部のみ。ゆえに実験では自由グルーオンではなくジェットとハドロニゼーションを見ます。
   • 観測：同方向にコリメートされたハドロンの雨。チャネル近傍ほどエネルギー集中。
3. 弱い相互作用の担い手（W・Z） — 厚い包絡で源近傍で散る
   • 性質：局在性が高く、結合が強く、寿命が短い波束。
   • 到達距離：発生地点の近くで伝達と崩壊を済ませ、特徴的な生成物の束を残します。
   • 観測：加速器での「瞬間の閃き」と多体崩壊の統計。
4. ヒッグス — 張力場のスカラー「呼吸」モード
   • 性質：海全体が「吸って吐く」ような体積的振る舞い。
   • 役割：この様式で励起できることの証拠です。本枠組みでは質量は安定結び目の自己維持コストと張力による案内から生じ、ヒッグスは特定の励起モードの証左です。

まとめの一文： ボソン＝波束。 遠くまで走るもの（光子）、チャネル内だけを走るもの（グルーオン）、源の近くで散るもの（W/Z、ヒッグス）がある。

IV. 巨視的な波束：重力波

• 定義： 巨大質量系が激しく組み替わると（合体・崩壊）、張力の地図が書き換わり、大規模なせん断リップルが海を駆け抜けます。
• 伝搬： ルールは同じで「張力が速度を、勾配が方向を決める」。物質との結合が弱いため、非常に遠方まで届きます。
• 観測： 干渉計における位相同期の「物差しの伸縮」、周波数が滑るチャープ、巨大構造を横切る際の同方向の時刻ずれ。

V. 「力」の起源：波束は粒子をどう動かすか

• 地形が変われば力が出ます。 波束が到着すると局所の張力がわずかに増減し、勾配が変わります。粒子はより「滑らか」な方向へ純漂移します。
• 多くは時間平均の効果です。 高速振動を時間平均して純効果が立ち上がります（放射圧、双極子トラップ、包絡駆動の輸送）。
• 選択的結合。 構造が合わなければほぼ素通り、合えば少量のエネルギーで強力に制御できます（光ピンセットなど）。
• 二つのガードレール。 局所の伝搬上限を超えないこと。常にフィードバックがあること（粒子・環境・波束が相互に変化）。

VI. 放射と吸収：三つの「合致」

• 周波数の合致： 放射体の内部リズムは特定の波束を吐き出しやすく、受信体のリズムが合えば取り込みやすい。
• 取向の合致： 方向性のある近傍場は、ある偏光を通し、反対は抑制します。
• 構造の合致： チャネルはチャネル波（グルーオン↔色束）を受け、厚い包絡は源近傍のみで作用し、光子はクリアウィンドウを長駆直入します。

VII. 複雑環境での「改装」

• 導波路とチャネル： 張力マップの低インピーダンス回廊が経路を整流します（極ジェット、星間フィラメントの集積帯）。
• 再処理と熱化： 「粗い海面」では多重散乱を受け、帯域が「すすけ」、鋭い線が分厚いスペクトルへ。
• 偏光の反転とねじれ： 取向化された媒質を通ると偏光がなめらかに回転、あるいは帯状に反転し、可読なカイラリティ標識を残します。

VIII. 身近な実験との対応

• 光子：偏光・干渉の検証、強重力レンズの時間遅延、パルサー／高速電波バーストに見られる無色散の共通遅延。
• グルーオン：高エネルギー衝突のジェット構造とハドロニゼーション・パターン。
• W/Z・ヒッグス：源近傍の短い閃光と崩壊生成物の統計。
• 重力波：干渉計での位相整合シグナルとメモリー効果。

IX. 主流理論と矛盾するか
いいえ。主流の枠組みは場と粒子の言葉で現象を高精度に算出します。本稿は同じ物理に対する物質的な説明図を与えるものです。

• 「場」はエネルギーの海の励起、「粒子」は自立する結び目。
• 「相互作用」は張力の書き換えと結合の選択性。
• 「不変な伝搬」は、環境間で張力により緩やかに変調されつつの局所不変。
  検証域では観測記述は一致し、どこが張り、どこが緩むか、なぜこの道は滑らかで別の道は詰まるのかを示します。

X. まとめ
波束はエネルギーの海を走る張力のしわであり、ボソンはそのファミリー、重力波は張力地形の大規模な反響です。共通の律は単純で強力です。張力が速度上限を、張力勾配が進行方向を与える。適合が結合の強さを決め、フィードバックがすべてを形作る。

図の読み方ガイド（誤解を避けるために）

I. 統一した読み取りルール

1. 曲線は「軌跡」ではありません。 曲線は**エネルギーの海（Energy Sea）**に生じる瞬間的な波形、すなわち張力のしわを示し、小粒子の通った道ではありません。
2. 矢印は伝搬方向です。 媒質内の点対点リレーによって模様全体が進み、次の瞬間には図形全体が矢印方向へ平行移動します。
3. チャネルあり／なし：
   • グルーオン： 色チャネルの内部だけを走ります（側面図：右に開いた淡色の「管」。内部の波形は管より明らかに狭い）。
   • 光子・W/Z・ヒッグス・重力波： 「管」はありませんが、局所の張力が定める速度上限と、その勾配による向きの制約を受けます。

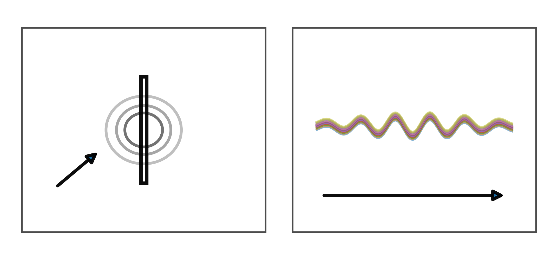
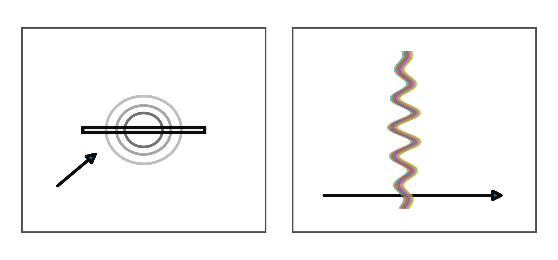
II. 光子 ― 線偏光（垂直／水平）

1. 正面図
   • 薄い同心円は等位相／スポット輪郭を示すだけで、偏光は表しません。
   • 細い短冊は電場 E の向きを示します（垂直または水平）。
   • 取り決め：k は伝搬方向、B は E と k の両方に垂直（矢印や点・バツ印で十分）。
2. 側面図
   • 垂直の線偏光： 伝搬方向に沿った細い正弦リボンを描き、その上下の振れで E の垂直振動を表します。曲線は位置に対する振幅の概略で、光の軌道ではありません。
   • 水平の線偏光： 立ち上がる細い正弦リボンを描き、その左右の振れで E の水平振動を表します。
   • いずれも k に垂直な平面内の運動で、横方向のせん断型のしわです。遠方界には k 方向の電場成分（縦偏光）は現れません。
3. 物理的ポイント
   • 自由空間の遠方界では E ⟂ B ⟂ k、かつ E と B は横方向平面内のみで変化します。
   • 近傍界や制限された導波路では k に沿う成分が現れ得ますが、それは束縛／導波モードであり、伝搬中の光子ではありません。
   • 光子は最も遠くまで届く波束で、張力がほぼ一様なら速度は「一定」に見えます。勾配に出会うと、経路依存の時間遅延や偏光回転などが生じます。

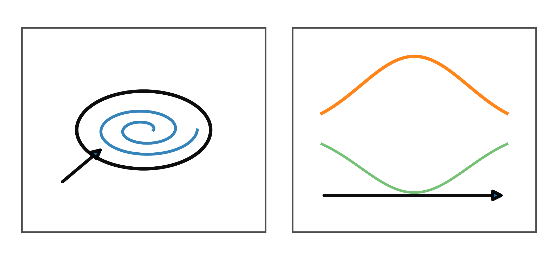
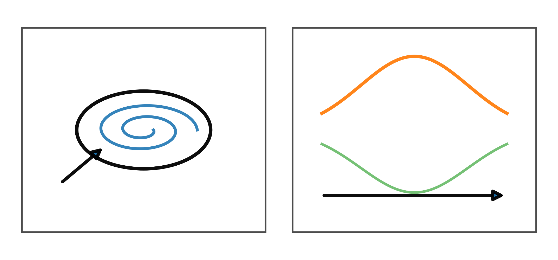
III. 光子 ― 円偏光（ヘリシティ）

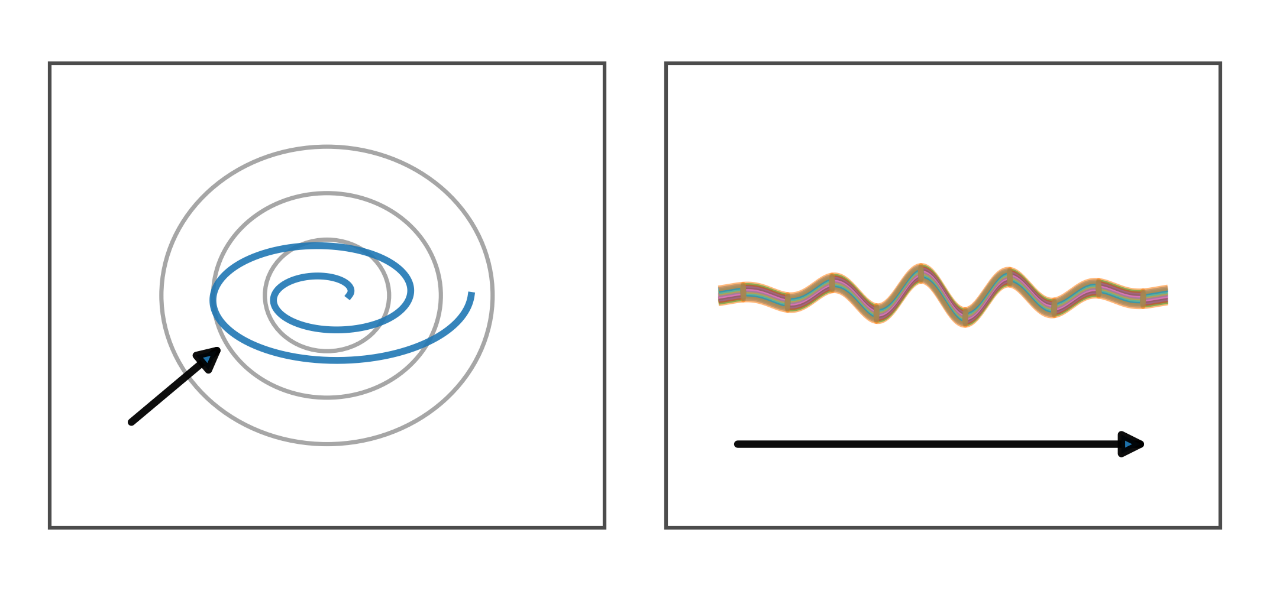
• 正面図： 小さなスパイラルで、横平面内の位相回転（左／右）を表します。
• 側面図： ゆるい螺旋感をもつ細いリボンが右へ進みます。螺旋は伝搬中の連続位相回転に由来します。
• 物理的ポイント： 円偏光は、キラルな媒質や配向した近傍構造と選択的に結合します。

IV. グルーオン ― 色チャネル内の伝搬

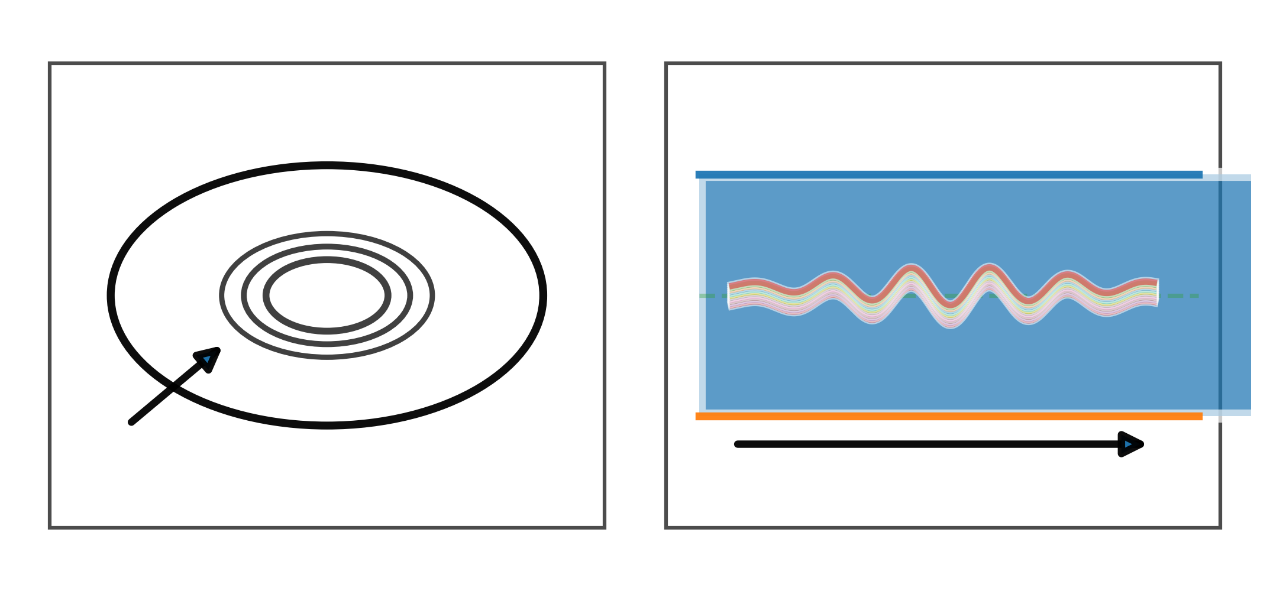
• 正面図： 楕円がチャネル断面で、内部の縞はその瞬間のエネルギーのうねりです。
• 側面図： 右に開いた淡色の長いチャネル本体。内部波形はチャネルより狭く、チャネルの中を走っていることを示します。
• チャネル内： 色拘束を受けるコヒーレントな波束が、フィラメント束に沿って導かれます。
• チャネル外： コヒーレンスが保てず、エネルギーは海へ戻り、周囲から糸が引き出されて許容される色中性の強子束へと閉じます。
• 観測されるもの： 「自由グルーオン」ではなく、ジェットとハドロニゼーションという再組織化の姿です。

V. W⁺／W⁻ ― 源近傍の厚い包絡

• 正面図： コンパクトな包絡にごく弱い螺旋模様（W⁺／W⁻ は逆巻きで区別）。
• 側面図： 対称な「ふくらんだ包絡」が数歩進んで減衰／解結合します。主要な作用は源の近くで完結します。
• 物理的ポイント： 強く結合し寿命が短い「厚い包み」で、遠くへ届く細波ではなく、局所の一撃に近い挙動です。

VI. Z ― ヘリシティの印を持たない厚い包絡

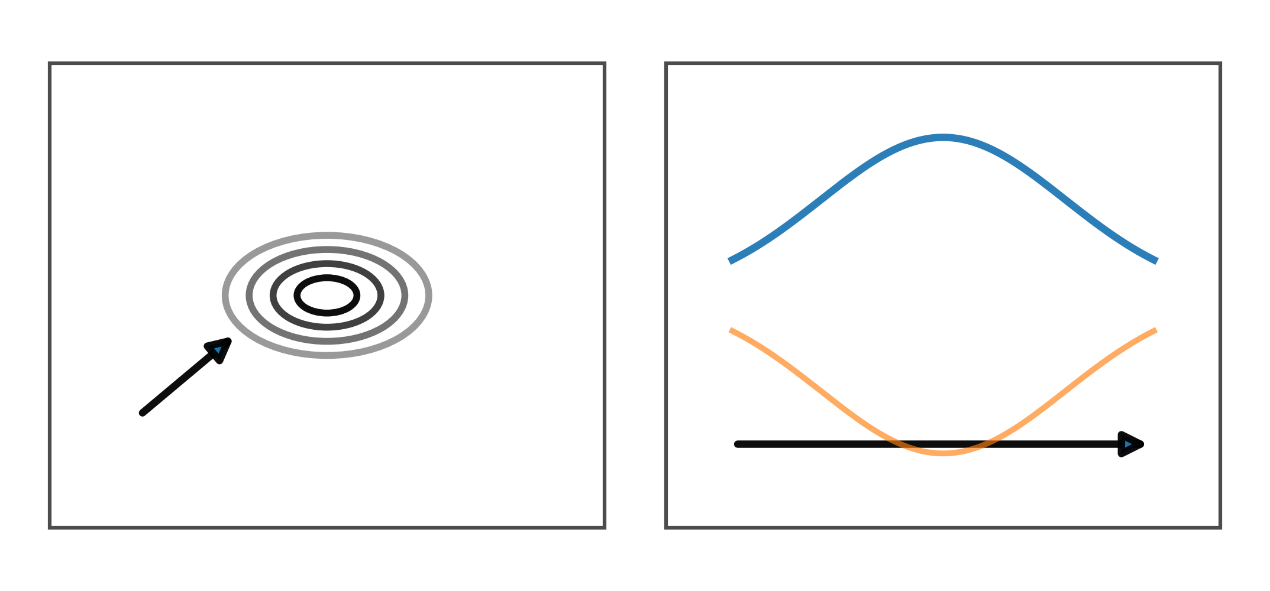
• 正面図： 同心の「呼吸」リングで、キラリティを強調しません。
• 側面図： W に近い厚い包絡で、さらに対称的に見えます。
• 物理的ポイント： こちらも源近傍で短距離の伝達を済ませ、安定な生成物へ解結合します。

VII. ヒッグス ― スカラーの「呼吸」波束

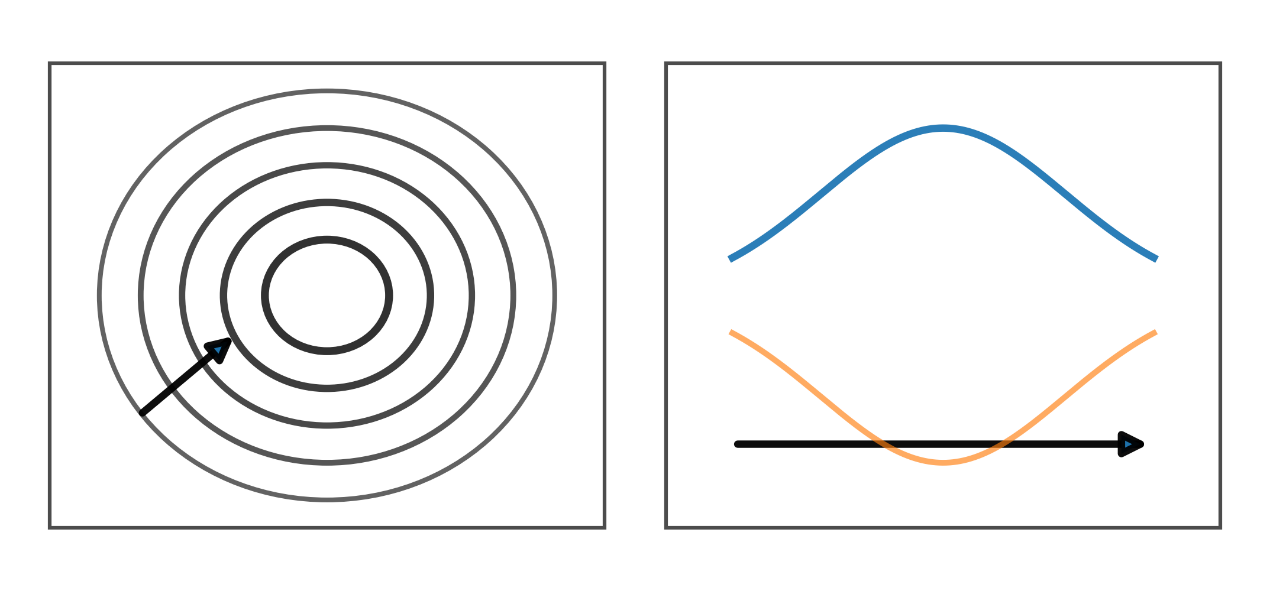
• 正面図： 複数の同心円が、張力の一斉な吸い込み／吐き出しを示します。
• 側面図： 幅広く対称な包絡が前進し、ほどなく散逸します。
• 物理的ポイント： 海がこのスカラー励起を支えることを示す存在証拠です。本枠組みでは質量は、安定結び目の自立コストと張力による案内から生じ、ヒッグスはそのモードの実証です。

VIII. 重力波 ― 張力の巨視的リップル

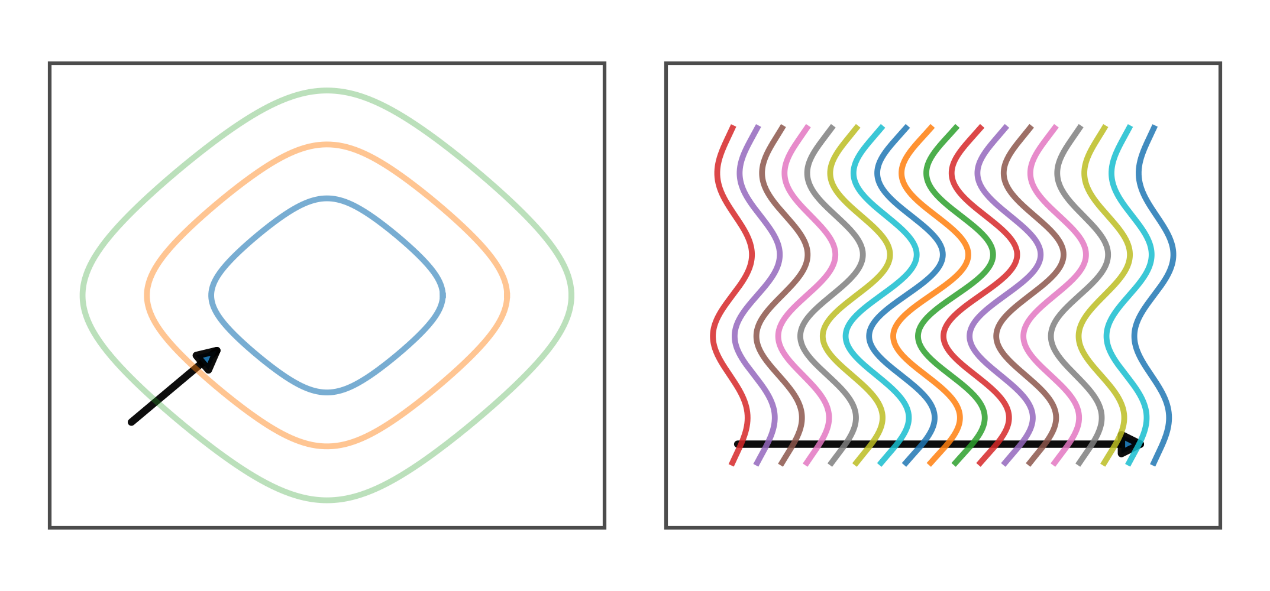
• 正面図： 伸長と圧縮が四象限で交互に現れる、典型的な四重極シグネチャ。
• 側面図： 垂直の「縞」が左右へやわらかくねじれ、全体として右へ進みます。
• 物理的ポイント： 物質との結合が弱く、非常に長距離を伝搬します。大規模構造を横切る際、経路依存の無色散な時刻オフセットが重なり得ます。